What Bayes rule is
Bayes Rule is a theorem that provides a way to update the probability of a hypothesis as new evidence is obtained.
It is named after Thomas Bayes, an 18th-century British mathematician and philosopher.
The theorem is stated mathematically as follows:
P(H|E) = [P(E|H) x P(H)] / P(E)
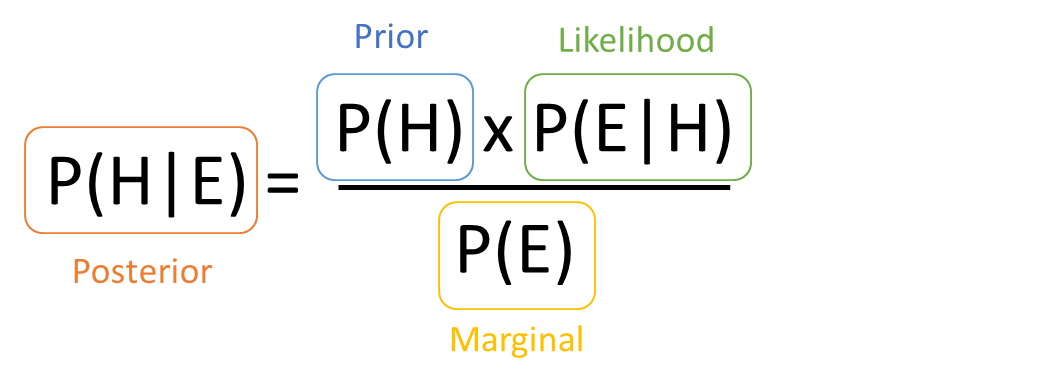
Where:
P(H|E) = posterior probability of the hypothesis given the evidence
P(E|H) = likelihood probability of the evidence given that the hypothesis is true
P(H) = prior probability of the hypothesis
P(E) = marginal probability of the evidence
To use Bayes Rule, one must:
-
Start with a hypothesis and determine the prior probability of the hypothesis (P(H)).
-
Collect evidence (E) related to the hypothesis.
-
Calculate the probability of the evidence given that the hypothesis is true (P(E|H)).
-
Calculate the probability of the evidence (P(E)).
-
Calculate the posterior probability of the hypothesis given the evidence (P(H|E)) using Bayes rule. This is the updated probability of the hypothesis.
-
Interpret the result.
Examples
-
Bayes rule can be used to calculate the probability that an event will occur, given certain evidence.
P(person has a disease | a positive test result)
-
Bayes rule can also be used to calculate the probability that a drug is effective, given the results of a clinical trial.
P(drug is effective | the results of a clinical trial)
-
Bayes rule can also be used to estimate the probability of a given outcome, given past data and a hypothesis.
P(customer will purchase a product | demographics, past purchases, and website activity)
Posterior probability
Posterior probability is a term used in Bayesian statistics to describe the probability of an event or hypothesis after considering new information or evidence.
It is the updated probability of an event, given the occurrence of a related event or information.
Examples of posterior probability
- Example 1:
- A medical test has a false positive rate of 5% and a false negative rate of 2%.
- If a patient tests positive for a disease, what is the probability that they actually have the disease?
P(actually having the disease | tests positive)
- Here, the prior probability of having the disease is the prevalence rate in the population,
- and the likelihood of observing the positive test result given the presence or absence of the disease is calculated.
- The posterior probability is the updated probability of having the disease after considering the test result.
- Example 2:
- A customer purchases a product from an online store and leaves a positive review.
- What is the probability that the product is of good quality?
- prior =
P(good quality product)
- prior =
- Here, the prior probability of the product being of good quality is based on the store’s reputation,
- and the likelihood of a positive review given the product’s quality is considered.
- likelihood =
P(positive review | good quality product)
- likelihood =
- The posterior probability is the updated probability of the product being of good quality after considering the positive review.
- posterior =
P(good quality product | positive review)
- posterior =